Regressão logística por gradient ascent
Neste post eu tento criar uma visualização que ajuda a entender como a regressão logística aprende a fronteira de decisão em um conjunto de dados.
O Problema da classificação
Podemos entender as técnicas de aprendizado supervisionado de máquina, de um modo bem amplo, como um conjunto de métodos empregados em dados para solucionar dois tipos de problemas: regressão e classificação.
Os modelos de classificação são utilizados quando a variável resposta é categórica. Assim, o modelo de regressão linear, por exemplo, se torna impróprio para realizar a classificação já que sua variável resposta é contínua.
O modelo de regressão logística é uma técnica bastante empregada e uma das mais conhecidas entre os modelos paramétricos supervisionados de classificação (obs: possui regressão no nome porém é utilizada para predizer variáveis categóricas), trata-se de um modelo linear com uma variável binária de resposta.
A intenção aqui é entender como os parâmetros da regressão logística são obtidos e então visualizar o procedimento da maximização da função de verossimilhança (likelihood), resolvendo programaticamente com o R as operações de álgebra linear e aplicando a técnica de otimização convexa por gradiente (gradiente ascendente, neste caso).
A função logística e probabilidade das classes
A função logística, também conhecida com sigmoid, nos permite conter os resultados de uma função linear entre 0 e 1. É esta função que recebe os parâmetros e variáveis na regressão logística e retorna as probabilidades de determinada observação do conjunto de dados pertencer a uma das classes.
sigmoid <- function(score) {
1/(1+exp(-score))
}
score = sigmoid(-5:5)
plot(c(-5,-4,-3,-2,-1,0,1,2,3,4,5), score, type = "l")
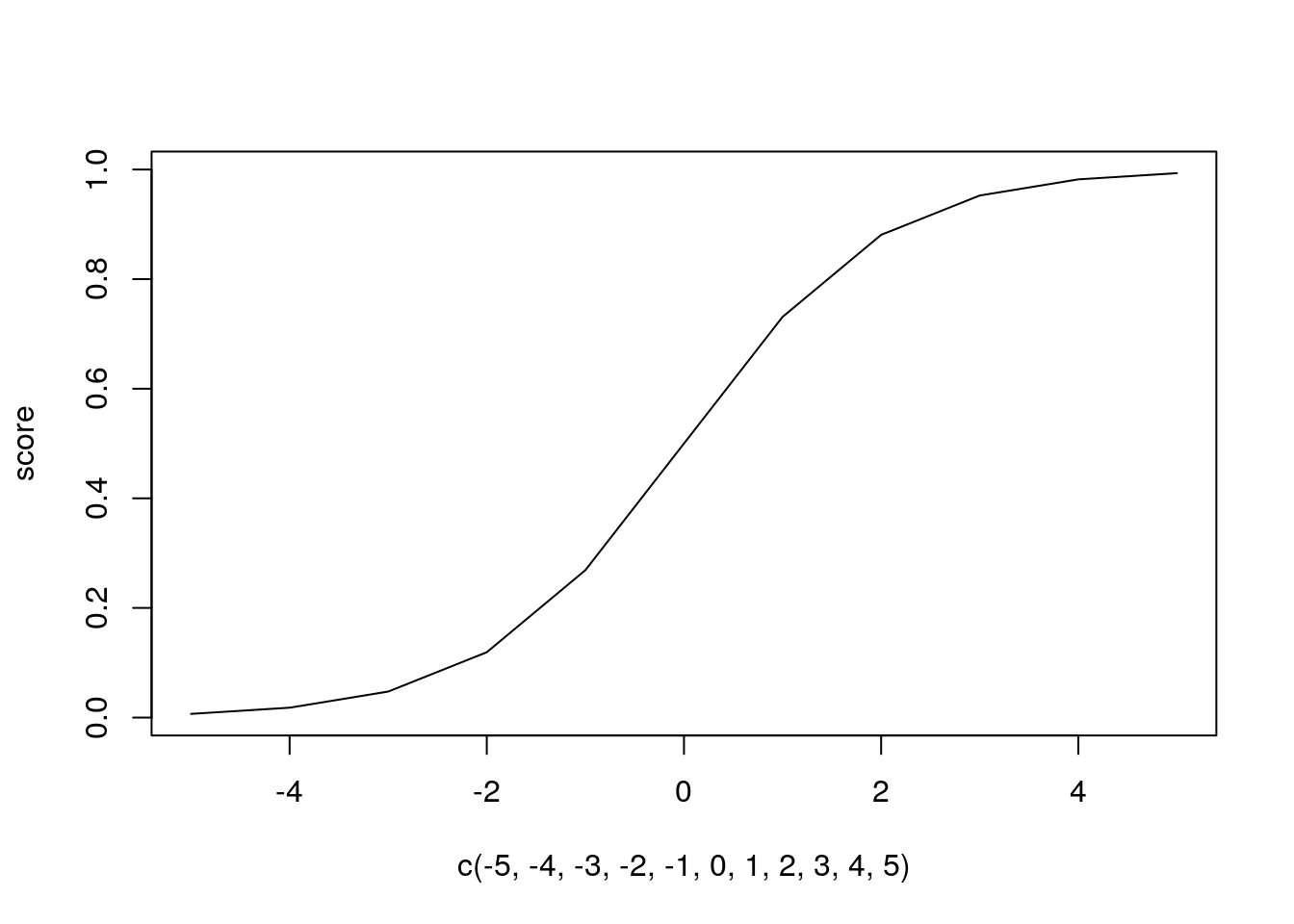
Na regressão logística, a probabilidade de uma observação do conjunto de dados pertencer à classe 1 condicionada conjuntamente pela matriz de variáveis X e pelo vetor de parâmetros θ - a probabilidade a posteriori - é dada por.
\[P(Y = 1| X, \theta) = \frac{1}{(1+\exp^{-\theta^T x})}\]onde o score é o produto escalar entre o vetor de parâmetros e a matrix de variáveis (aqui levando em conta o intercepto x0 = 1):
\(\theta^Tx = \theta_0 + \sum_{i=1}^{m}\theta_i x_i\) a implementação fica assim:
sigmoid <- function(theta, X) {
1/(1+(exp(-(X %*% theta))))
}
A estimação dos parâmetros
Os parâmetros são obtidos pela otimização da função da likelihood. O objetivo é escolher coeficientes θ que maximizam:
\[L(\theta) = \prod_i^n P(y_i|X_i, \theta)\]Tomar o logaritimo da função facilita a manipulação daqui pra frente. O produtório se torna somatório e as operações com o exponencial se tornam mais simples:
\[LL(\theta)=\sum_{i=1}^{n}lnP(y_i|x_i,X_i,\theta)\]A função de log likelihood (log da verossimilhança) da regressão logística então tem a seguinte forma, onde yi pode assumir os valores do conjunto discreto {0,1}, o primeiro termo, como já vimos, é a probabilidade de yi assumir o valor 1 e o segundo termo é a probabilidade de yi assumir o valor 0:
\begin{align} LL(\theta)&= y_i ln\frac{1}{(1+\exp^{-\theta^T x})}+(1-y_i)ln\frac{exp^{-\theta^Tx}}{(1+exp^{-\theta^T x})} \newline &= \sum_{i=1}^{n}{(y_i-1)\theta^Tx_i - ln(1+exp^{\theta^Tx_i})} \end{align}
A implementação pode ser feita da seguinte forma, notem q o produto escalar de X e theta equivale ao produto escalar da transposta de theta com x:
loglikelihood <- function(X,y,theta) {
score <- X %*% theta
logexp <- log(1+exp(-score))
sum((y-1)*score - logexp)
}
Gradient steps
O logaritimo da função de likelihood é uma função convexa. O objetivo então é encontrar o ponto máximo desta função à partir de sua derivada, atualizando o valor dos coeficientes (theta) a cada iteração até atingir a convergência. É esperado que a cada iteração o valor da função log-likelihood aumente até “estabilizar”.
O gradiente nos dá a “direção” do máximo da função. Precisamos obter a derivada desta função nos coeficientes e então aproximar a derivada para zero.
\[\frac{\partial ll(\theta)}{\partial \theta_j} = \sum_{i=1}^{N}x_i(y_i- \frac{1}{(1+\exp^{-\theta^T x})})\]A equação a seguir nos mostra a atualização dos coeficientes a cada iteração. O eta(η) é o tamanho do passo que damos na direção (gradiente) do ponto de otimização do coeficiente theta j. Também é chamado de learning rate e é um parâmetro de extrema importância, já que dependendo de sua magnitude a convergência torna-se muito demorada ou até impossível. Aqui ele será escolhido de forma arbitrária e fixo em todas as iterações, porém existem diversos métodos que podem ser encontrados na literatura de otimização que tratam só da escolha do learning rate adaptativo.
O sobrescrito t indica que o theta atual é uma atualização do theta obtido na iteração anterior t-1.
\(\theta_j^{t} = \theta_j^{t-1} + \eta\frac{\partial ll(\theta^{t-1})}{\partial \theta_j^{t-1}}\)
Tanto a derivação quanto a atualização dos thetas serão implementados na função que chamei de gradient. A cada iteração os thetas estimados e o likelihood serão armazenados no data frame df_bystep.
gradient <- function(X, Y, theta, step_size, iter) {
y <- X %>% dplyr::select(all_of(Y))
mtx <- X %>% dplyr::select(-all_of(Y)) %>% mutate(intercept = 1) %>% as.matrix()
derivative <- c()
df_bystep <- data.frame()
for (i in 1:iter) {
e = (y) - (sigmoid(theta, mtx))
for (j in 1:ncol(mtx)) {
derivative[j] = sum(mtx[,j]*e)
theta[j] <- theta[j] + (step_size*derivative[j])
}
llkh <- loglikelihood(mtx, y, theta)
df_bystep <- rbind(df_bystep, c(theta, llkh, i))
}
names(df_bystep) <- c(colnames(mtx), "loglikelihood", "iteration")
df_bystep
}
Visualizando o gradient ascent
Por fim, todas as funçoes que foram implementadas até aqui serão executadas para realizar uma classificação de dados.
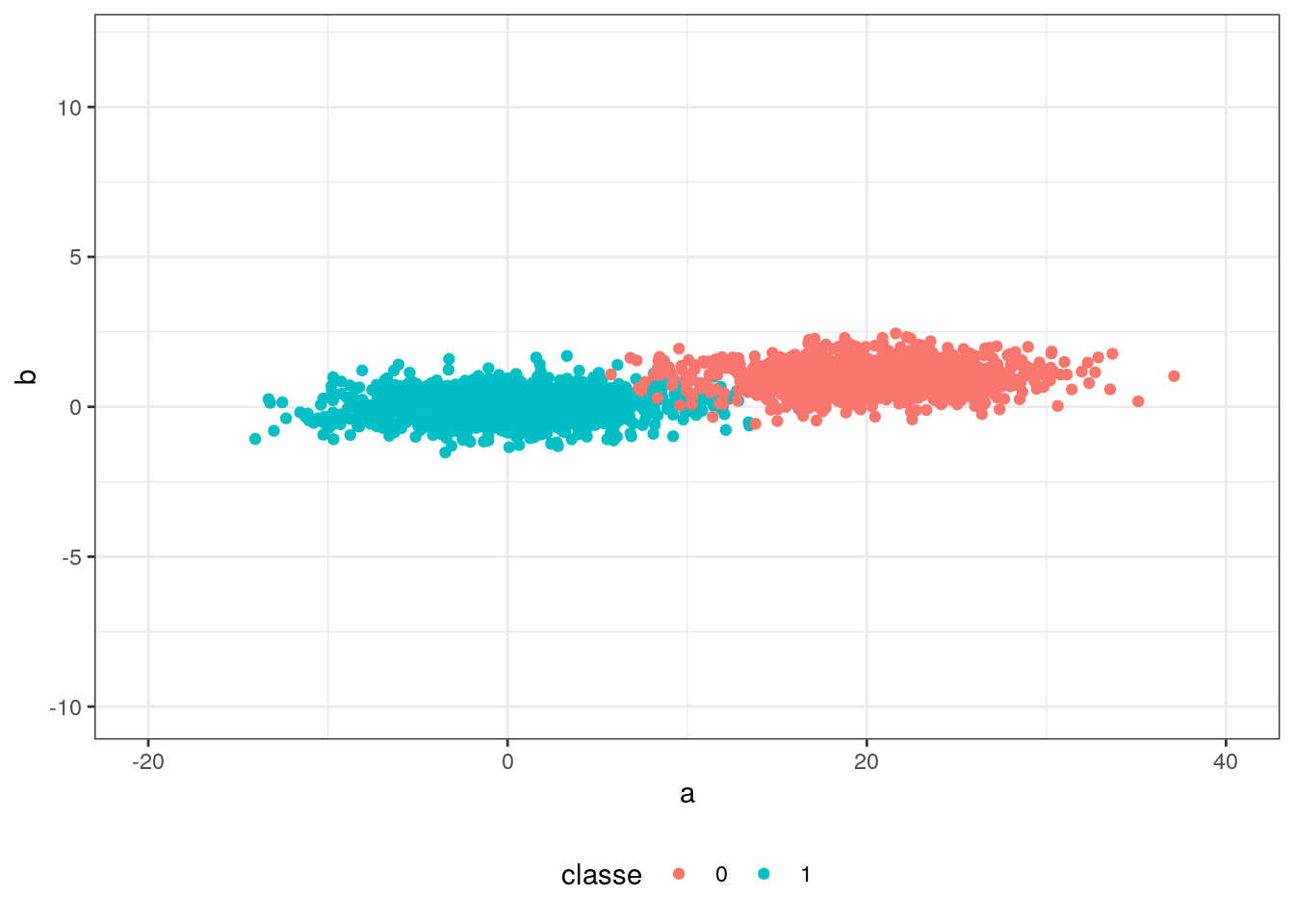
Os dados utilizados serão bem simplificados: duas variáveis (a e b) com observações que podem pertencer a duas classes (0 e 1) geradas por um processo aleatório normalmente distribuido. A intenção é facilitar a visualização do ajuste do hiperplano.
set.seed(123)
a1 <- c(a = rnorm(1000, 0, 5))
b1 <- rnorm(1000, 0, 0.5) %>% cbind(b = ., classe = 1)
a0 <- c(a = rnorm(1000, 20, 5))
b0 <- rnorm(1000, 1, 0.5) %>% cbind(b = ., classe = 0)
df <- data.frame(a = c(a1, a0),
rbind(b1, b0))
ggplot(data = df, aes(a, b)) +
geom_point(aes( colour= factor(classe)))+
xlim(-20, +40) +
ylim(-10,12)+
labs(colour = "classe") +
theme_bw()+
theme(legend.position="bottom")
Os parâmetros passados para a função são: conjunto de dados, nome da variável de interesse, coeficientes theta iniciais, step size e quantidade de iterações:
gd <- gradient(df, "classe", c(0,0,0), 0.0003, 200)
O objeto gd agora armazena um data frame com informaçẽos de cada uma das iterações, a e b e intercept são coeficientes obtidos naquela iteração, loglikelihood é a verossimilhança obtida:
tail(gd)
## a b intercept loglikelihood iteration
## 195 -0.4914219 -1.322780 4.913247 -118.9108 195
## 196 -0.4185990 -1.322451 4.925506 -116.6961 196
## 197 -0.4899070 -1.328619 4.925460 -118.0654 197
## 198 -0.4205768 -1.328425 4.937352 -116.1138 198
## 199 -0.4883971 -1.334411 4.937538 -117.2564 199
## 200 -0.4225749 -1.334352 4.949062 -115.5454 200
Partindo daqui fica fácil visualizar o processo. Eu utilizei o pacote gganimate para gerar as animações e depois juntei todas as gifs em uma imagem só. O resultado é esse:
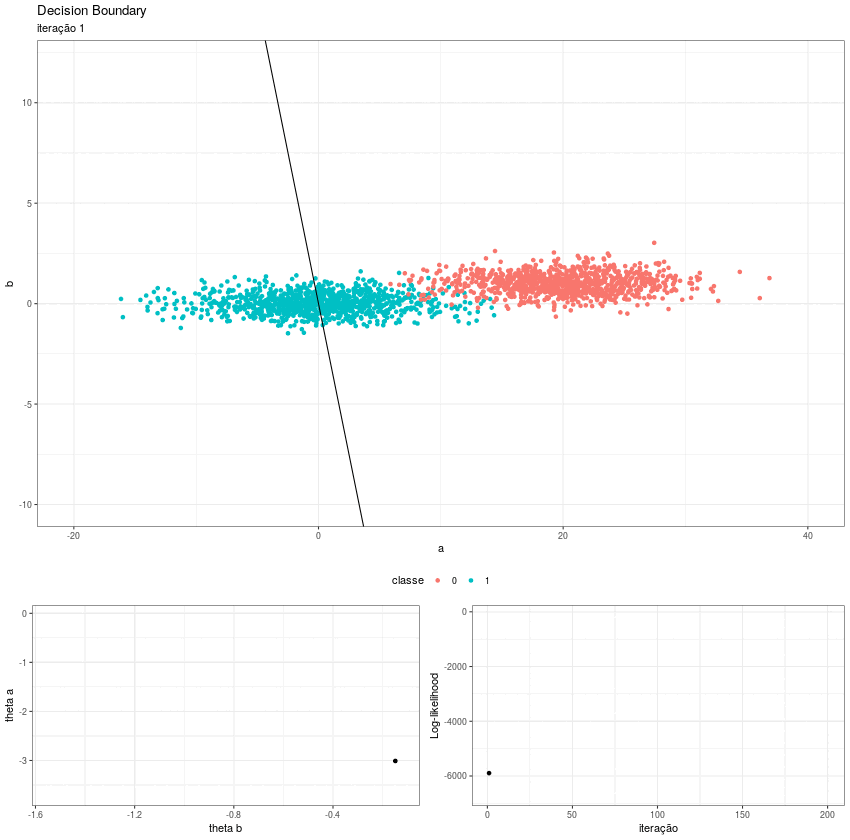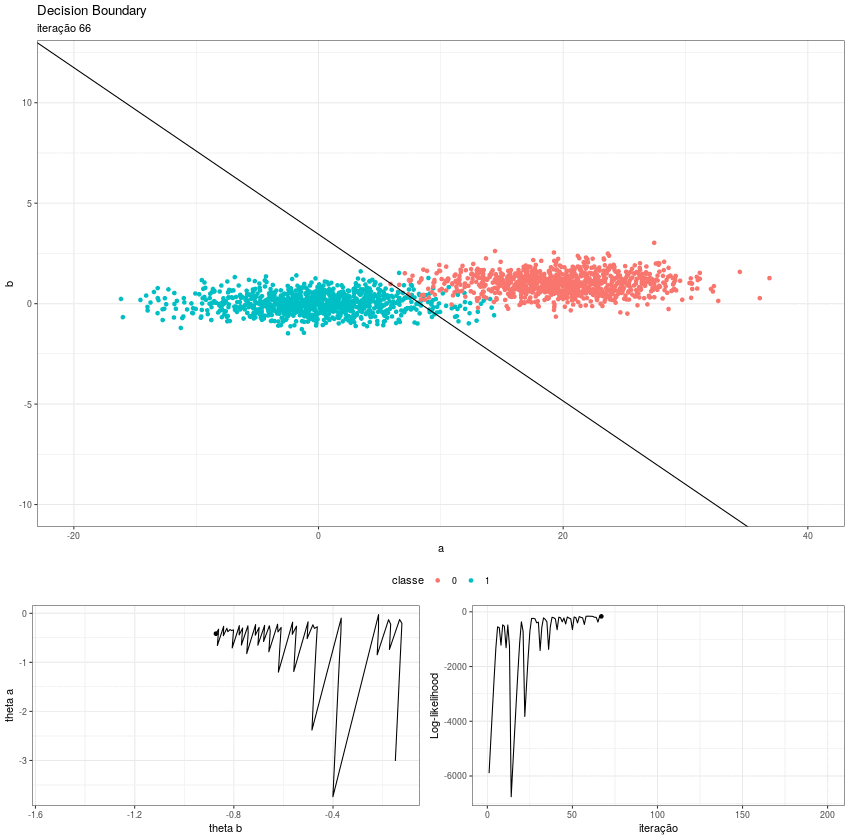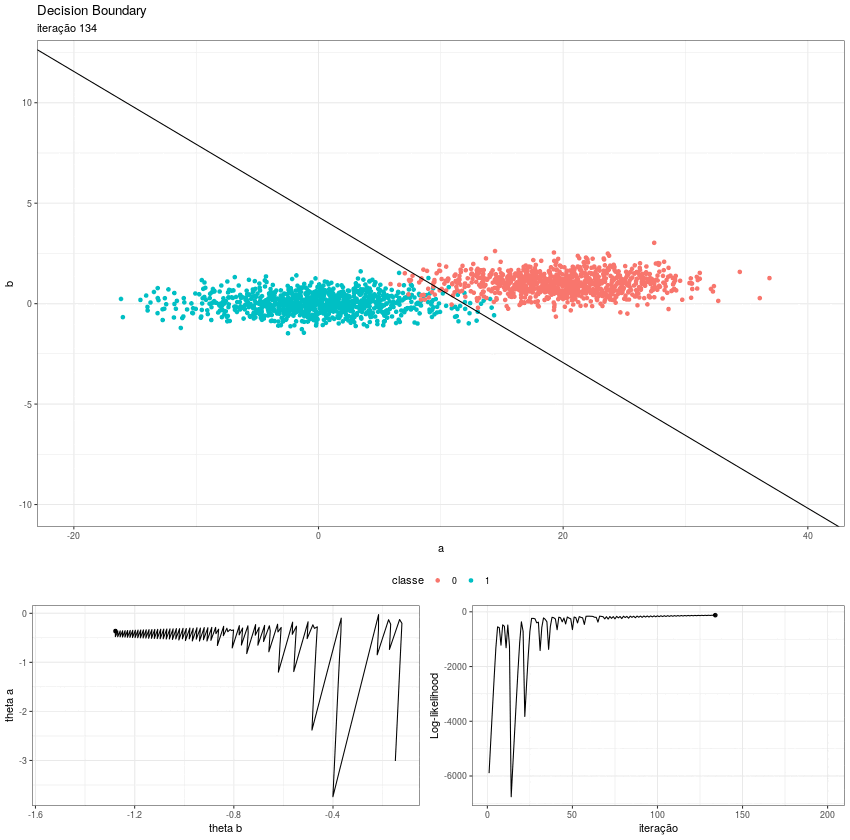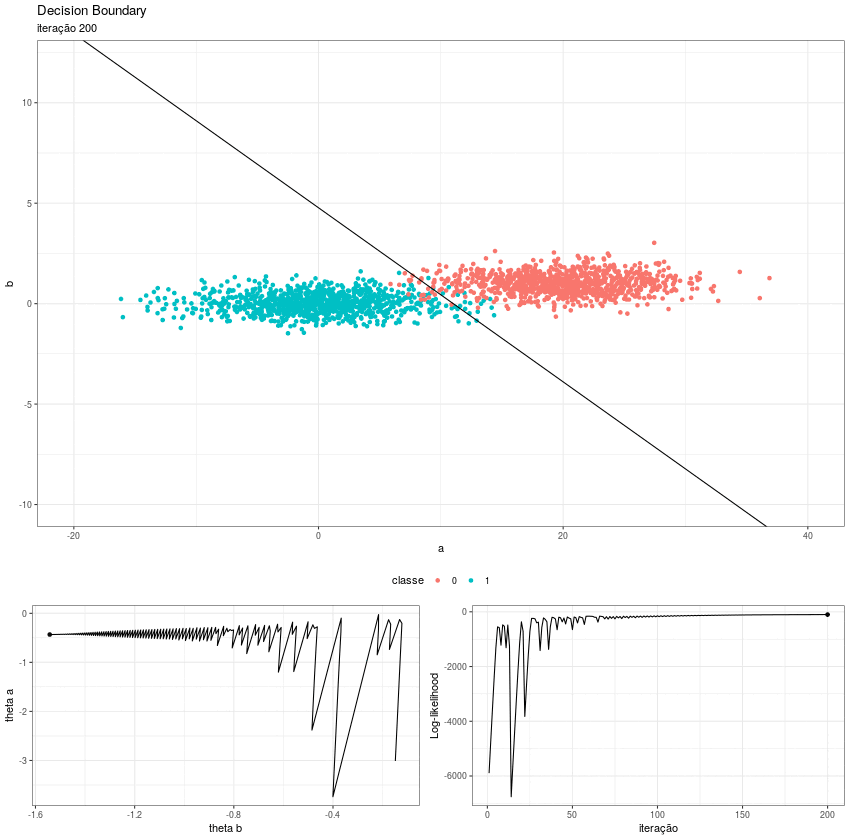
No primeiro quadro vemos a fronteira de decisão se ajustando, podemos perceber como o intercepto funciona como um “centro de massa” do hiperplano; no segundo, o algoritmo converge para os thetas ótimos e no terceiro a função de log likelihood caminha para seu máximo.
Esse zigue-zague se deve ao eta. Se escolhermos um step size menor, o caminho se torna mais liso, porém a convergência é bem mais lenta.
Considerações
A otimização por gradient raramente é utilizado na regressão logística em pacotes estatísticos/machine learning. No capítulo 4 do “The elements of statistical learning”, os autores discutem algumas técnicas que se aproximam do que é utilizado no mundo real. Porém, mesmo se tratando de uma técnica simples, podemos através dela compreender os conceitos gerais do classificador binário e o exercício de implementar um conceito é sempre desafiador.
Código utilizado para gerar as animações:
library(gganimate)
library(ggplot2)
library(dplyr)
library(magrittr)
decisionb <- ggplot(data = df, aes(a, b)) +
geom_point(aes( colour= factor(classe)))+
xlim(-20, +40) +
ylim(-10,12)+
geom_abline(data = filter(gd, iteration <=200), aes(intercept = intercept, slope = a)) +
labs(colour = "classe", title = "Decision Boundary", subtitle = "iteração {as.integer(frame_time)}") +
theme_bw() +
theme(legend.position="bottom")+
transition_time(iteration)
anim_decisionb <- animate(decisionb, width = 850, height = 600, nframes = 200, end_pause = 15)
anim_save("anim_decisionb", anim_decisionb)
theta <- ggplot(data = filter(gd, iteration <=200), aes(x=b, y=a))+
geom_path()+
geom_point()+
xlab("theta b") + ylab("theta a") +
theme_bw()+
transition_reveal(iteration)
atheta <- animate(theta, width = 425, height = 240, nframes = 200, end_pause = 15)
anim_save("atheta", atheta)
llgg <- ggplot(data = filter(gd, iteration <=200), aes(x=iteration, y=loglikelihood))+
geom_path()+
geom_point()+
xlab("iteração") + ylab("Log-likelihood") +
theme_bw() +
transition_reveal(iteration)
allgg <- animate(llgg, width = 425, height = 240 , nframes = 200, end_pause = 15)
anim_save("allgg", allgg)